早嶋です。
意思決定のツール「バラつきの概念」では、標準偏差のお話をさらっと書きましたので、今回は少し掘り下げてみます。
先ず、バラつきとは何か?を考えて見ましょう。前回の例で、中央区のパン屋さんの顧客のリピート購買回数をもとに考えてみます。中央区のパン屋さんの例では、顧客①~顧客⑩までの来店回数を示しました。これら10人の来店回数の平均値は100回です。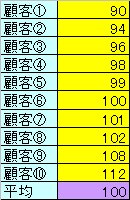
しかし、レンジ(最小値と最大値の差)を見てみると最小回数が90回、最大回数が112回と言うことで、それぞれ平均値の100回から離れているものや近いものまでバラバラですね。このようにバラつきとは、ある値(平均)を基準に、他の値がどのくらい乖離(離れているか)しているかを示すものです。
バラつきを調べるためにレンジを調べることは有効ですが、限界がありますね。レンジでは、最小値と最大値の差分を見ているだけなので、個々のデータを調べているわけではないからです。そこで、登場するのが標準偏差になるわけです。標準偏差を求める式を眺めていたら、少しびっくりするので、どのような考え方なのかを見てみましょう。
バラつきとは、個々のデータが平均からどの程度離れているか?を示すものなので、バラつきを定量的に求めるために、個々のデータと平均値の距離を調べて、その距離の合計値が大きいほどバラつきが大きいということがいえますね。
パン屋さんの例で考えましょう。顧客①と平均値の距離は、-10、顧客②と平均値の距離は-6、・・・顧客⑩と平均値との距離は12となります。上記の図を見てもわかるとおり、距離の乖離には正負が含まれているので、単純に合計すると相殺される可能性がありますね。
バラつきが大きければ、平均値からの距離の合計が大きい!ということは感覚的に判りますが、正負があるので単純には足すことが出来ない。このときの考え方として、1)絶対値の合計を取る、2)それぞれの距離を2乗して合計を取る、がありました。
1)の方が簡単そうですが、数学や統計の世界では何故か、2)が採用されました。2)の考え方で正負の問題は解消できますが、合計値で常に考えるのでは、扱うデータの数が常に同じでないと比較が出来ないですね。そのため、合計値の数をデータの数で割っているのです。このようにする事で、データの個数が異なっても比較する事ができますね。
数学では、この状態の値を分散と呼びますが、まだまだ問題があります。それは、単位がなくなることです。個々のデータの平均値の距離を2乗した時点で単位がなくなってしまいます。そこで、基のデータと比較できるように、平方根を取ってあげる作業をすると良いのです。
このように考えると、標準偏差の式に2乗が出てきたり、ルートが出てきたりする事が理解できると思います。