早嶋です。
「数値とカテゴリ」では、数値データをざっくり見るために、代表値の紹介をしました。数値データの代表値は、平均や中央値、最頻値など、カテゴリデータの代表値は割合や比率でしたね。
今回は、その中でも平均に注目してみます。例えば、次のような事例を考えて見ましょう。
あなたは今、中央区(①)と東区(②)の両方にパン屋を展開しているビズナビベーカリーのオーナーだとします。ビズナビベーカリーは地域に密着したベーカリーショップを目指しているために、顧客のリピート率を1つの経営指標として様々な意思決定を行っています。
さて、そのような中、あなたは、①と②の今年度の顧客リピート回数を年間100回と設定しました。そして、①と②では、それぞれの顧客データの蓄積により、目標を達成したと報告がありました。
【報告内容】
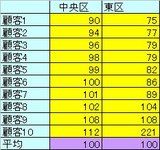
①、②の店舗とも顧客数は10人。その顧客のリピート回数を調査して、それぞれ平均を出したところ丁度、100回だった。
さて、①と②、共に目標を達成したと言えるでしょうか?今回のゴールは、顧客のリピート回数を100回を上回ることですので、平均を見る限り、①も②も満たしていますね。
では、どちらがより確実に目標を達成しているといえるでしょうか?それを調べるために、「バラつき」を見てみましょう。平均値が同じならば、全てのお客様が平均の100回に近い回数をリピートしている方が望ましいといえるでしょう。
1)レンジ(幅)を見る
ざっくり把握するためには、レンジを見ましょう。レンジは、データを昇順か降順に並べて最大値と最小値の差を見ることです。
①の場合、最小90回で最大112回なのでレンジは22ですね。同様に、②の場合、最小75回で最大が224回なのでレンジは146です。
レンジを調べるだけで、②の方がバラつきが大きいことがわかりますね。
では、バラつきをもっと的確に表現するにはどうすると良いでしょうか?コレが、小学校のときに習った標準偏差です。標準偏差=バラつきを表す1つの指標、と考えればOKです。
2)標準偏差を計算する
計算方法は割愛して、①の標準偏差は6.41、②の標準偏差は43.97となります。コレを見ると明らかに②>①なので、②の方がバラつきが多いということがわかります。
パン屋さんの例では、リピート回数の目標達成に対して、平均というアプローチと標準偏差というアプローチの2つを取りました。平均値だけでは、①と②のバラつきがどの程度なのか?を考慮していないことがわかります。
実際の経営環境では、平均値は多く使われますが、ある異常値が全体の平均値を上げる(又は、下げる)動きをしていることが良くあります。しかし、標準偏差でバラつきまで把握しておけば、そのようなことも防ぐことが出来るのです。
統計では、データの全体像を捉えるために、平均と標準偏差をセットで用いることが良くあります。